El tetraedro
El objetivo de este proyecto es que aprendas a construir tu primer Alquimetrico.
Construir ALQUIMÉTRICOS implica trabajar en 3 dimensiones, aquí te guiaremos en la construcción del poliedro regular más simple posible.
Con solo 4 conectores y 6 varillas, puedes construir un tetraedro de una sola punta. ¿Crees que este es el poliedro regular más simple que existe?
Es imposible construir una estructura 3D cerrada de cara plana con menos conectores o varillas. Pertenece a las familias de sólidos platónicos y piramidales, porque sus caras triangulares se encuentran en un vértice común en la parte superior.
MATERIALES NECESARIOS
- 4 conectores hexagonales
- 6 varillas (12 para el tetraedro de doble varilla)
- 12 tiras elásticas
Bajar contenidos
FICHA TÉCNICA
- Duración: 30'
- Disciplina:
- Matemática – Figuras, cuerpos geométricos: reconocimiento y análisis de sus características. Prismas y pirámides, relaciones entre sus elementos: vértices, caras y aristas.
- Artes – Elementos del lenguaje.
- Prácticas del lenguaje – Escritura compartida y autónoma.
- Nidel de dificultad: Bajo/Medio
- Licencia: Creative Commons 4.0 atribución.
- Créditos: Tati Tabak, Fernando Daguanno, Carlos Vidal, Luciana Squeri, Léo Melo, Alquimétricos 2020/2021
Prerrequisitos
- ANTES DE COMENZAR
Todo lo que precisas saber para elegir y utilizar correctamente los materiales y herramientas necesarios para hacer tus Alquimétricos. - REPRODUCIR MOLDES
En el caso de que no tengas cómo imprimir el diseño de los moldes provistos. - FABRICAR MOLDES
Siempre es bueno tener distintos moldes listos antes de comenzar a profucir conectores. - FABRICAR CONECTORES
El bloque fundamental de toda construcción alquimétrica son los conectores y las varillas. La salsa secreta está aquí… - ENCASTRES
Conoce y experimenta con las diferentas formas de vincular conectores y varillas, o crea las tuyas y compártelas aquí.
Contenidos curriculares
Video
Instrucciones detalladas para la construcción del Tetraedro.
Instrucciones paso a paso.
01
Elegir un conector hexagonal y ensarta una varilla pasándola por los dos agujeros que hay en uno de sus vértices. Entrando por encima de la figura y saliendo por debajo.
02
Pasar una segunda varilla de la misma manera en uno de los vértices adyacentes.
03
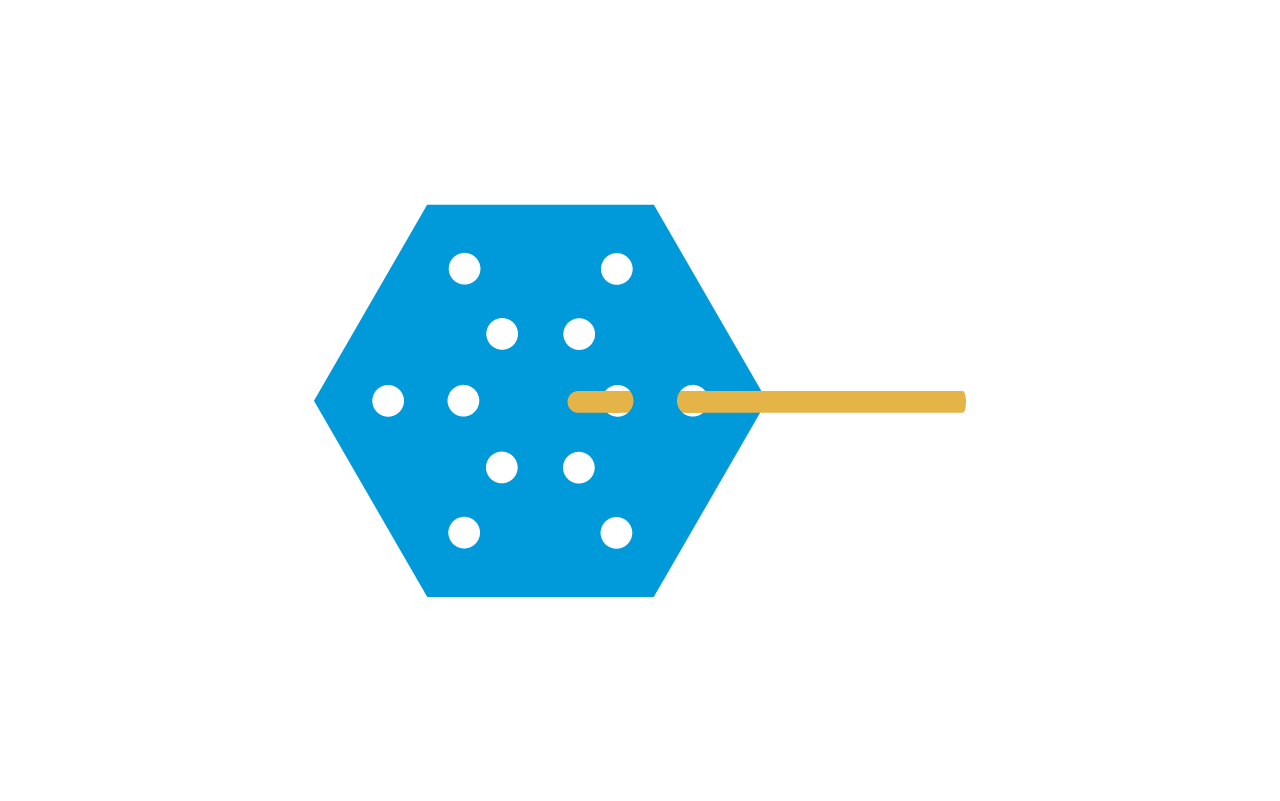
Colocar los conectores en los extremos libres de cada una de las varillas utilizadas.
04
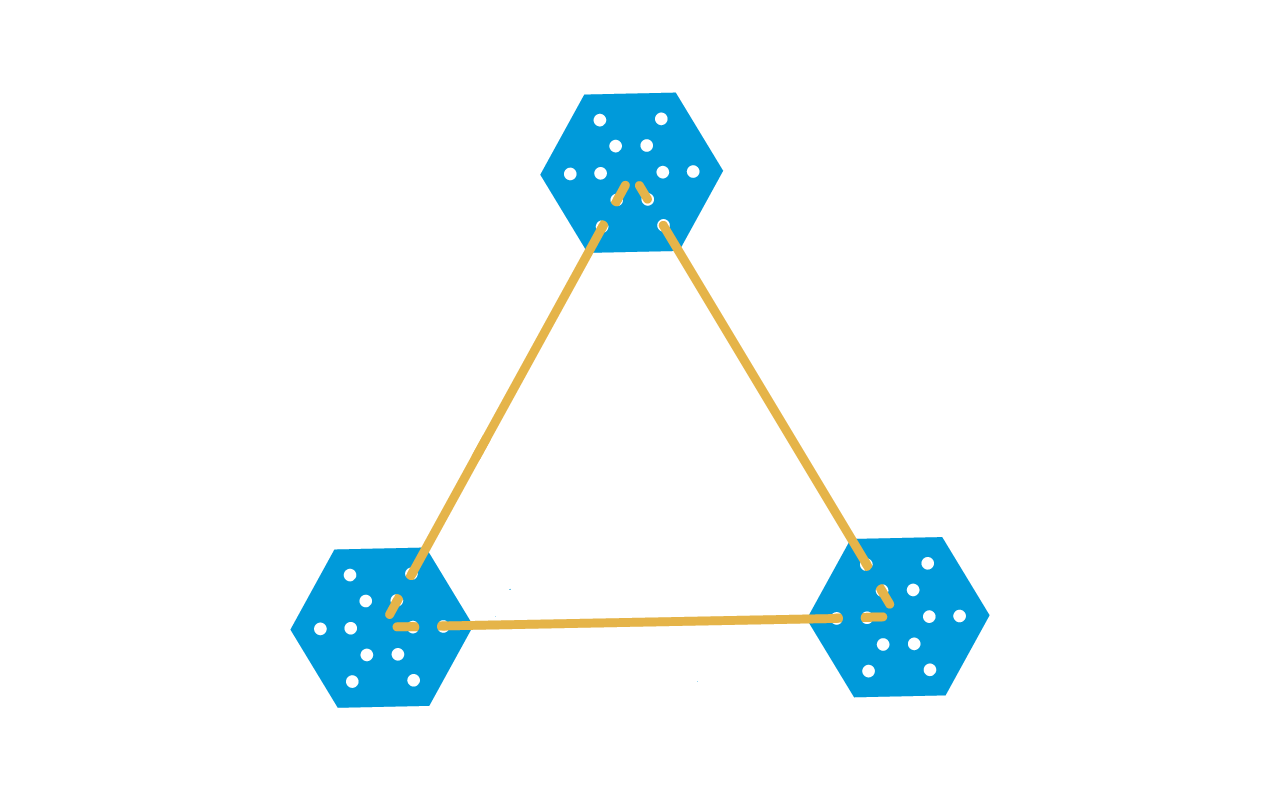
Unir los dos conectores colocados en el paso anterior, con una varilla nueva, formando un triángulo.
05
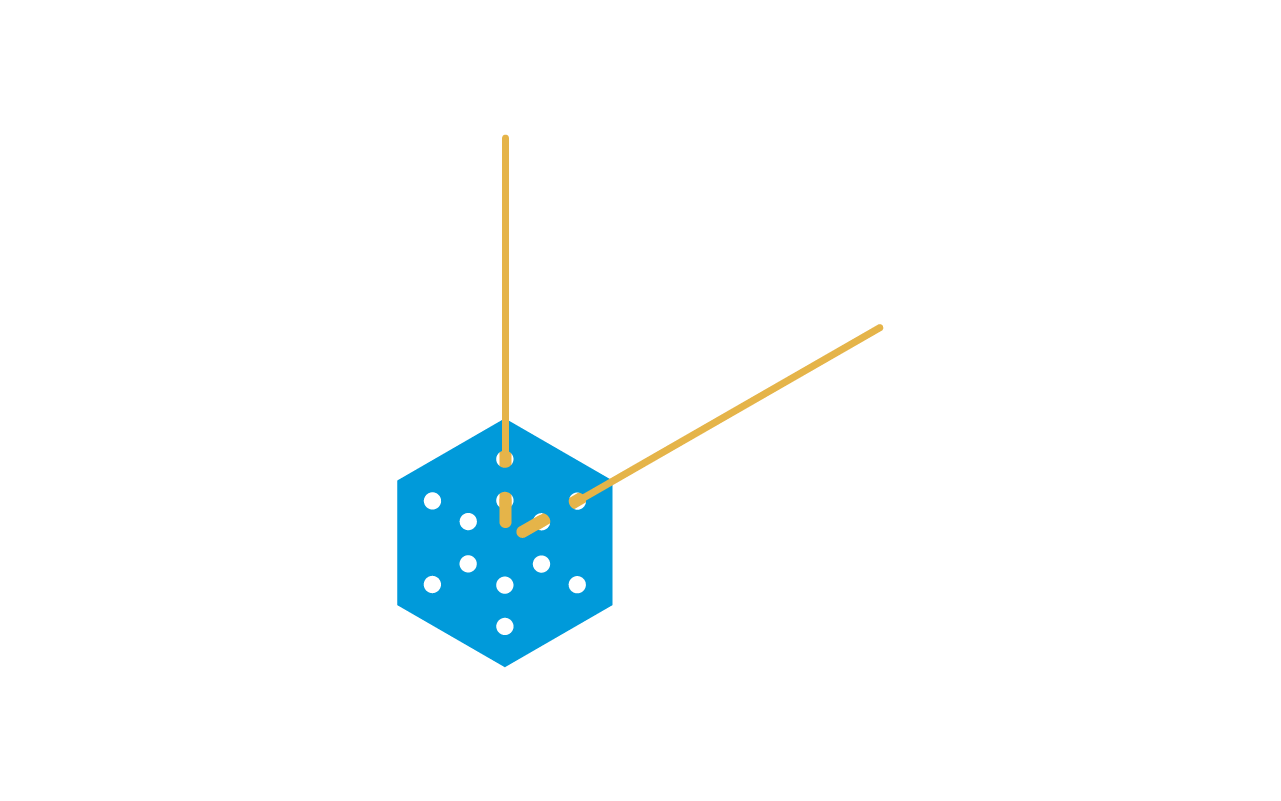
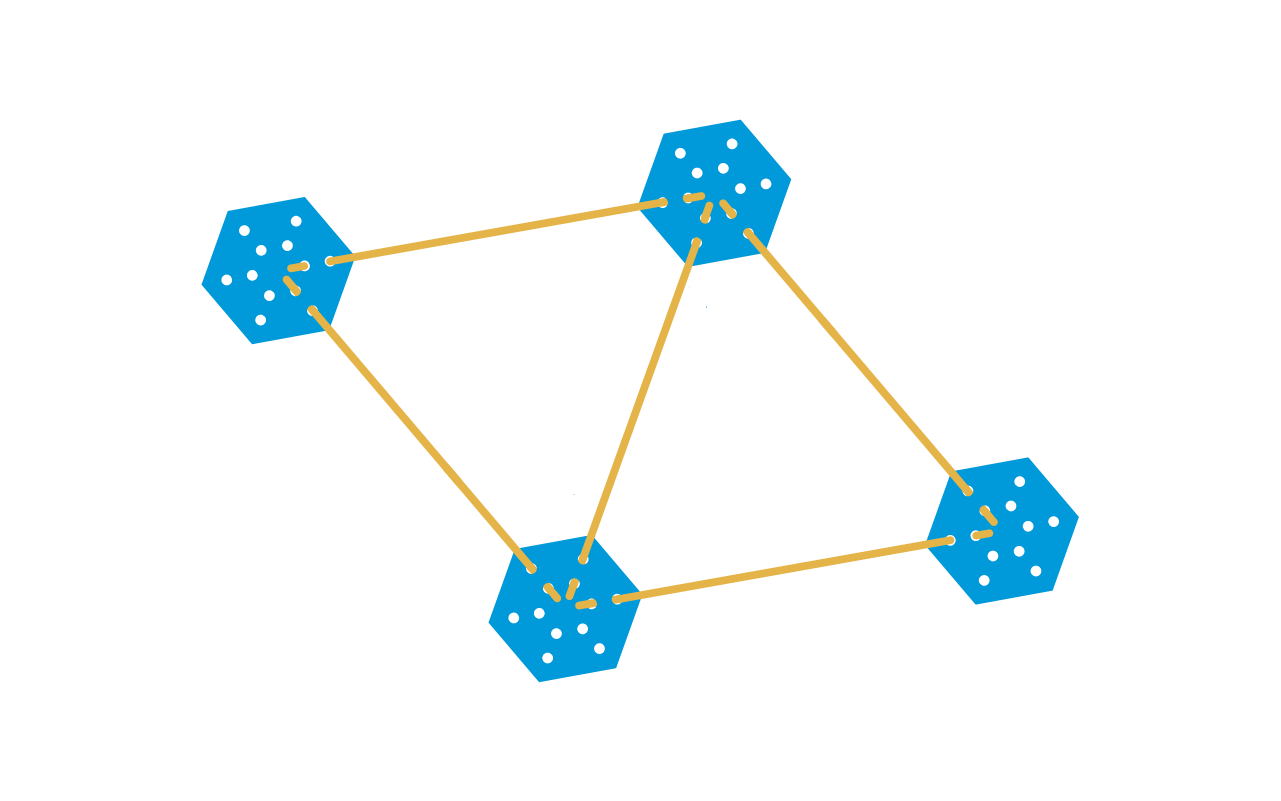
Elegir dos de los hexágonos y enhebrar una varilla en cada uno. Unir estas dos nuevas varillas con un cuarto conector.
06
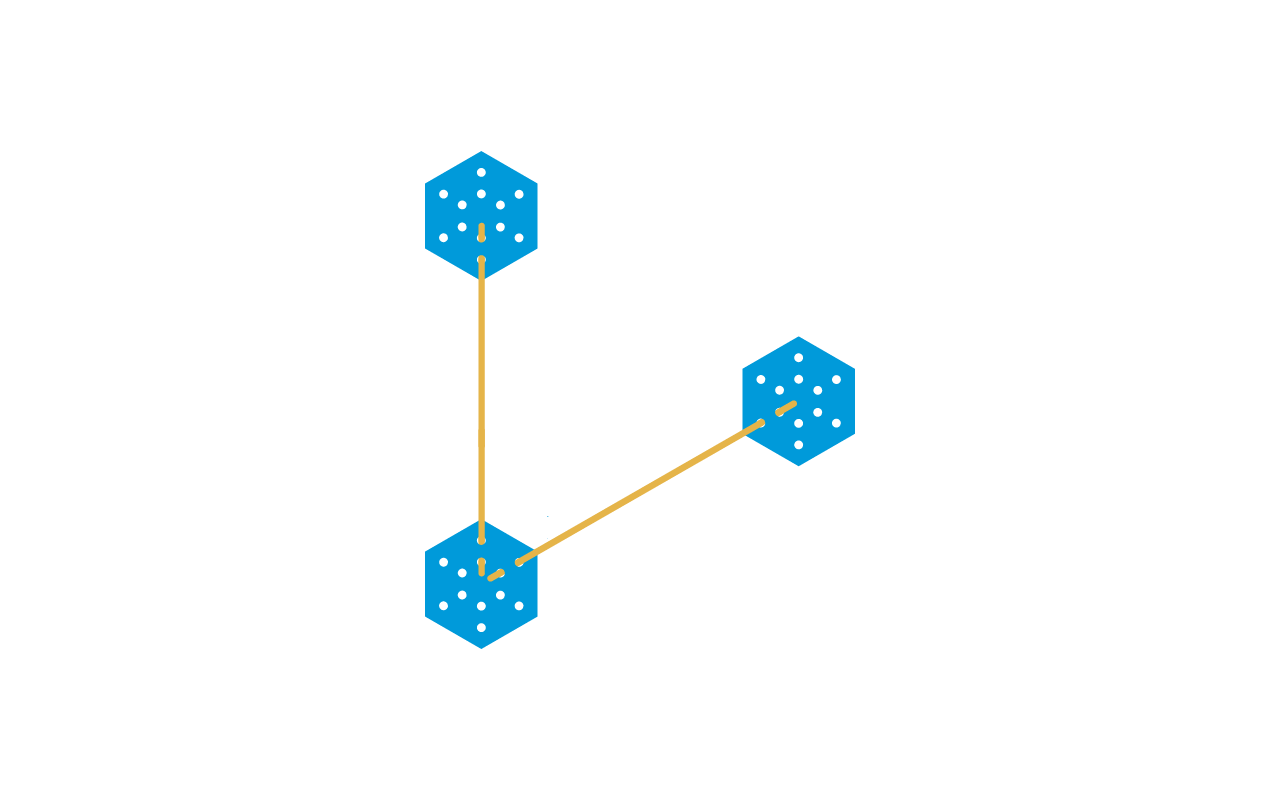
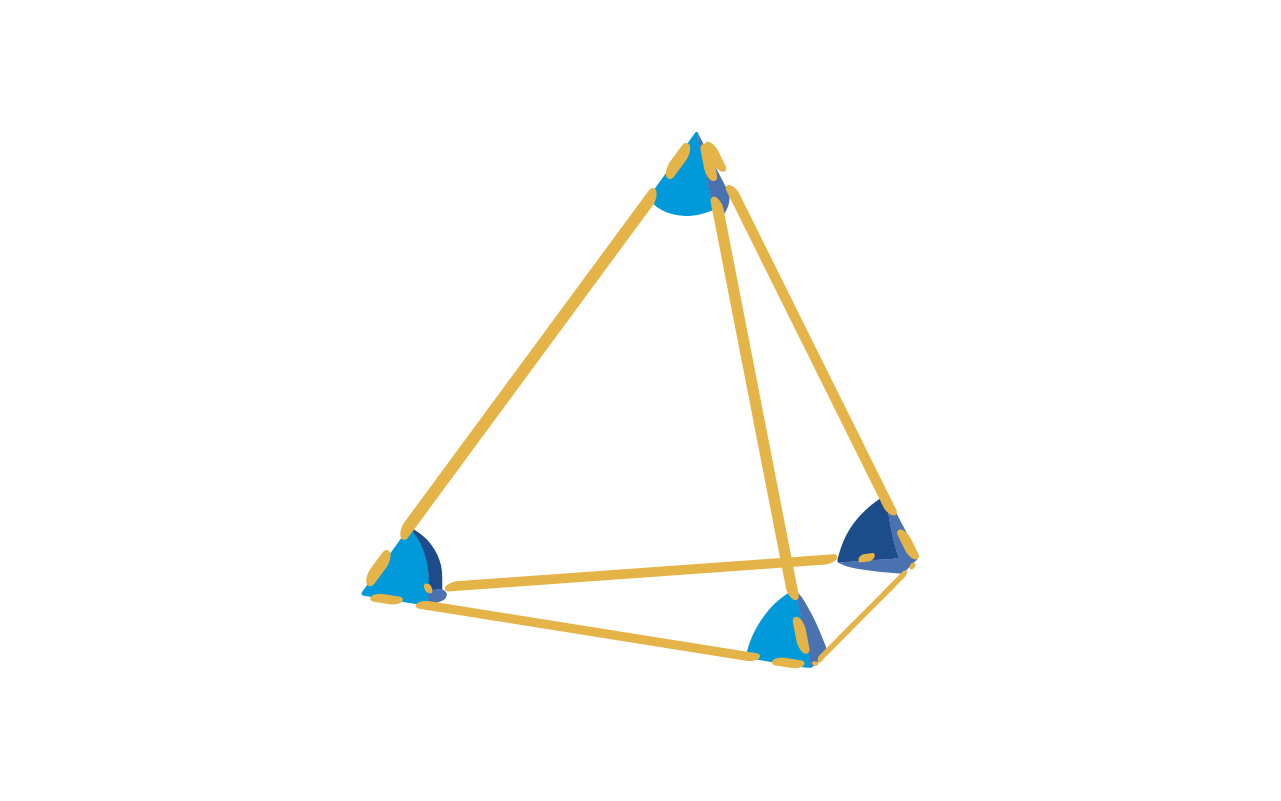
Adjuntar este nuevo y último conector al hexágono que dejamos sin usar en el paso 5.
ATENCIÓN:
Si usas dos varillas en orificios contiguos para unir cada par de conectores, puedes lograr un resultado visualmente más atractivo y estructuralmente más sólido.
ATENCIÓN;
Si el agujero es más grande que el palillo, puedes usar los mini elásticos para asegurar la unión.
Para continuar aprendiendo.
De cuerpo a figura y de figura a cuerpo:
- Se puede abordar a partir de la identificación de las figuras planas (en este caso los triángulos equiláteros) que forman la figura y tratando de identificarlos en otros objetos tridimensionales cotidianos.
- Es posible proponer una reflexión sobre cuáles son las propiedades de las figuras planas utilizadas que permiten construir cuerpos regulares de este tipo y tratar de predecir con cuál de las figuras se pueden ensamblar cuerpos similares.
Elementos gráficos y formas geométricas:
- Explora, reconoce e identifica los elementos visuales: punto, línea, forma, espacio, relieve, movimiento, volumen bidimensional y tridimensional, tanto en la figura construida como en los objetos de la casa con los que esta figura se puede comparar.
Lectura y escritura:
- Es posible reflexionar sobre la importancia de identificar los aspectos centrales de una lista de pasos y probar las derivaciones de cambiar el orden de las instrucciones.
- Se pueden utilizar diferentes estrategias para la elaboración de instrucciones para el montaje del tetraedro, considerando diferentes situaciones y lectores.
